Where the techniques of Maths
are explained in simple terms.
Algebra - Absolute values - graphs.
Test Yourself 2.
- Algebra & Number
- Calculus
- Financial Maths
- Functions & Quadratics
- Geometry
- Measurement
- Networks & Graphs
- Probability & Statistics
- Trigonometry
- Maths & beyond
- Index
| Transformations | 1. (i) Graph y = |x| (ii) Write the equation transformed from y = |x| where there is a horizontal shift of 2 to the right and a shift of 1 down. (iii) Graph the transformed equation. |
2. (i) Write the equation transformed from y = |x| where there is a horizontal dilation of 2 and a horizontal shift of -1. (ii) Graph the transformed equation. |
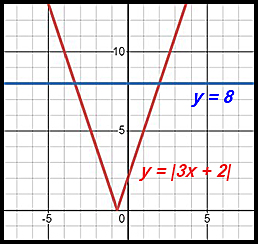
| Graph the two components of each of the following equations on the same set of axes. So for Q3, graph y = |3x + 2| and y = 8. On the basis of your graph, solve the given equation for x value(s). Check you answers with the corresponding question number in Absolute Value equations TYS 1. | ||
| 3. |3x + 2| = 8
|
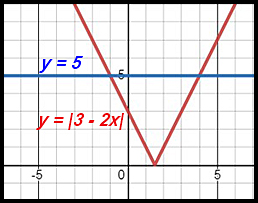
4. |3 - 2x| = 5
|
|
| 5. |-2x - 3| = 7
|
6. | |
| 7. | 8. | |
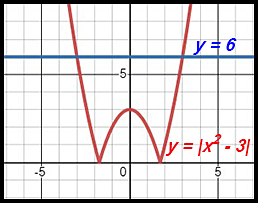
| Solving equations graphically. | 9. |x2 - 3| = 6
|
10. |x2 + 3| = 8
|
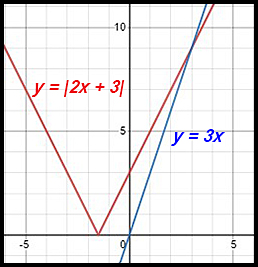
11. |2x + 3| = 3x
NOTE: The lines only cross once - so x = -0.6 cannot be a solution. |
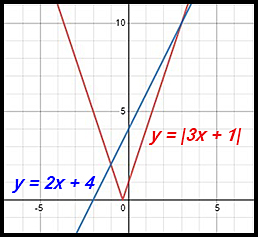
12. |3x + 1| = 2x + 4
|
|
13. |4 - 2x| = x - 2
|
14. |2x + 5| = 3x + 9
|
|
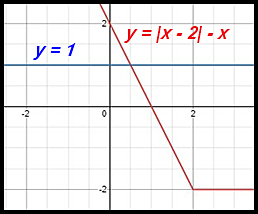
15. |x - 2| - x = 1
|
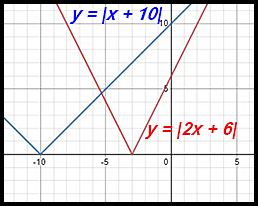
16. |2x + 6| = |x + 10|
|
|
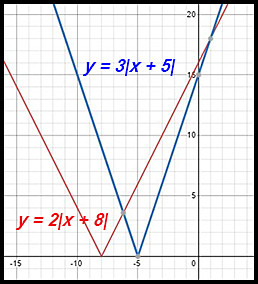
17. 2|x + 8| = 3 |x + 5|
|
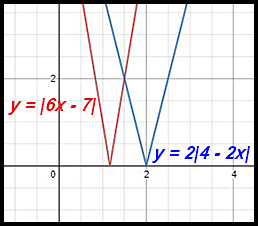
18. |6x - 7| = 2|4 - 2x|
|
|
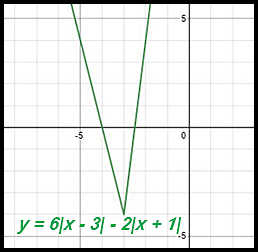
19. 6|x + 3| - 2|x + 1| = 0 Two graphs are drawn for comparison: (i) Here we are looking for the solution where the graph crosses the x axis as the equation was given as the LHS = 0. Solutions at x = -4 and |
(ii) Graphing the two components separately and then equating them at the points of intersection:
Here we are looking for the two points of interesction because we have equated the components. Again the solutions shown by these points of intersection are at x = -4 and at x = -2.5. |
|
20. (i)
|
(ii) Finding all values for k for which the equation The gradient of the lines are +2 and -2 respectively. |
|
|
||